This post is part of a What Is… series that explains spatial audio techniques and terminology.
The last post was a brief introduction to Ambisonics covering some of the main concepts of first-order Ambisonics. Here I’ll give an overview of what is meant by Higher Order Ambisonics (HOA). We’ll be sticking to the more practical details here and leaving the maths and sound field analysis for later.
Higher Order Ambisonics (HOA) is a technique for storing and reproducing a sound field at a particular point to an arbitrary degree of spatial accuracy. The degree of accuracy to which the sound field can be reproduced depends on several elements: the number of loudspeakers available at the reproduction stage, how much storage space you have, computer power, download/transmission limits etc. As with most things, the more accuracy you want the more data you need to handle.
Encoding
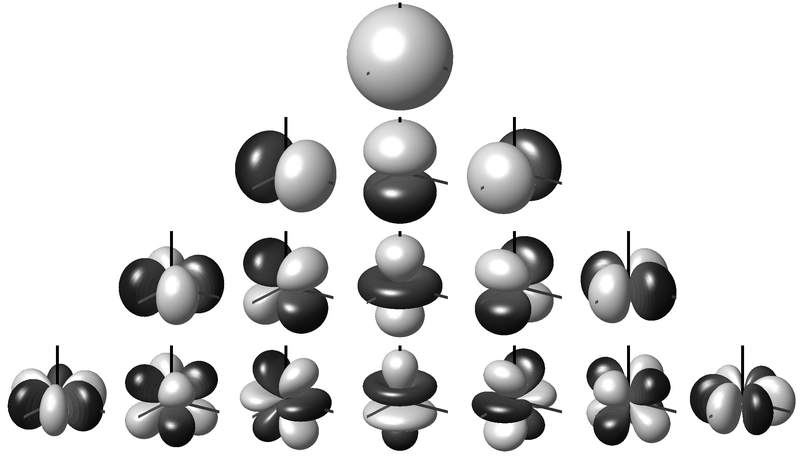
In its most basic form, HOA is used to reconstruct a plane wave by decomposing the sound field into spherical harmonics. This process is known as encoding. Encoding creates a set of signals that depend on the position of the sound source, with the channels weighted depending on the source direction. The functions become more and more complex as the HOA order increases. The spherical harmonics are shown in the image up to third-order. These third-order signals include, as a subset, the omnidirectional zeroth-order and the first-order figure-of-eights. Depending on the source direction and the channel, the signal can also have its polarity inverted (the darker lobes).
An infinite number of spherical harmonics are needed to perfectly recreate the sound field but in practice the series is limited to a finite order \(M\). An ambisonic reconstruction of order \(M > 1\) is referred to as Higher Order Ambisonics (HOA).
An HOA encoded sound field requires \((M+1)^{2}\) channels to represent the scene, e.g 4 for first-order, 9 for second, 16 for third, etc. We can see that very quickly we require a very large number of audio channels even for relatively low orders. However, as with first-order Ambisonics, it is possible to do rotations of the full sound field relatively easily, allowing for integration with head tracker information for VR/AR purposes. The number of channels remains the same no matter how many sources we include. This is a great advantage for Ambisonics.
Decoding
The encoded channels contain the spatial information of the sound sources but are not intended to be listened to directly. A decoder is required that converts the encoded signals to loudspeaker signals. The decoder has to be designed for your particular listening arrangement and takes into account the positions of the loudspeakers. As with first-order Ambisonics, regular layouts on a circle or sphere provide the best results.
The number of loudspeakers required is at least the number of HOA encoded channels coming in.
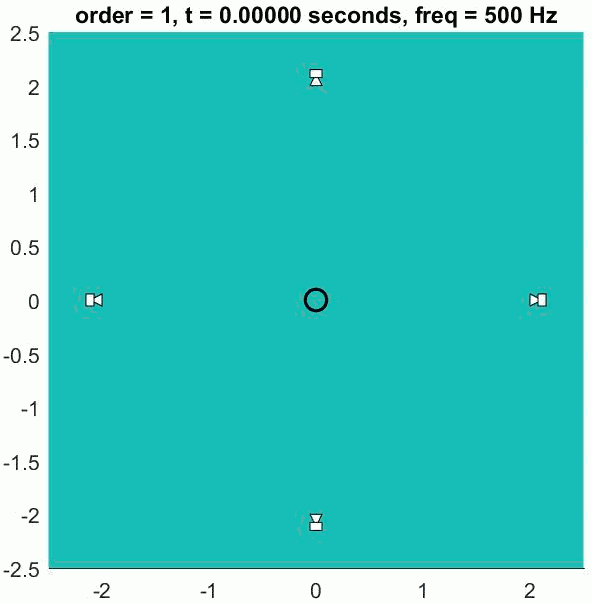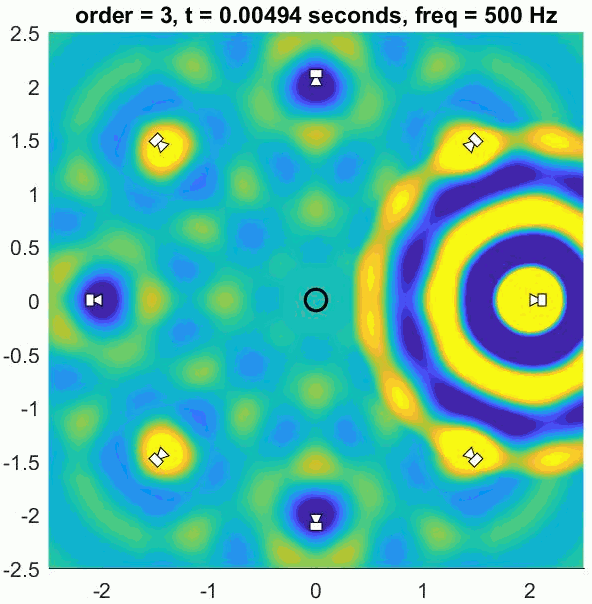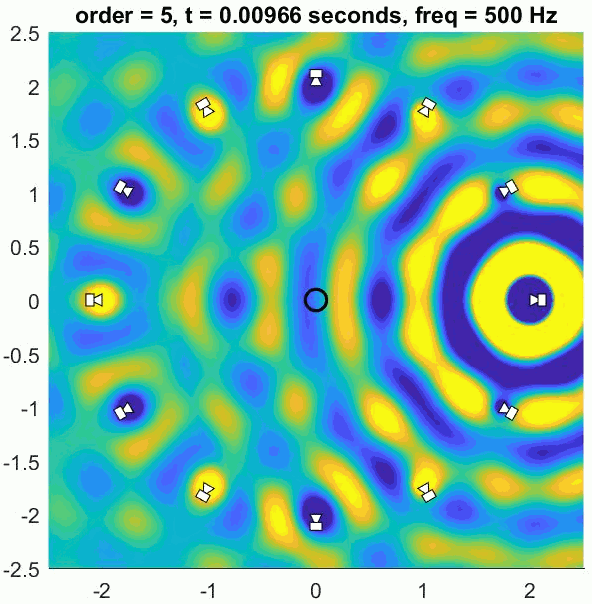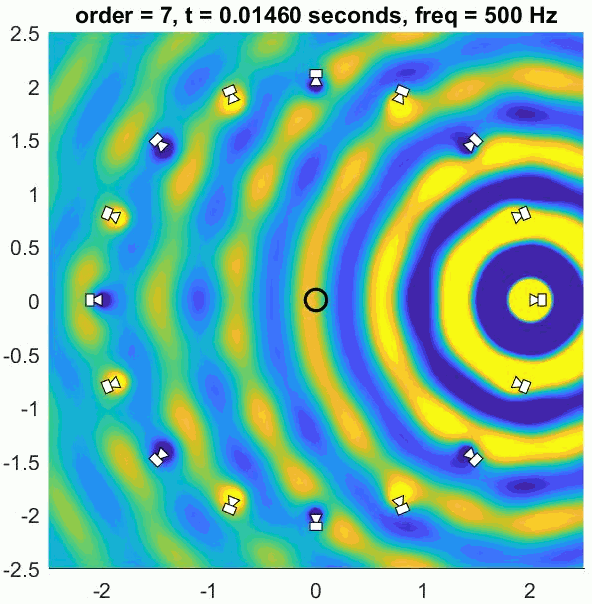
A so-called Basic decoder provides a physical reconstruction of the sound field at the centre of the array. The size of this physically accurately reconstructed area increases with increasing order but decreases with frequency. Low frequency ranges can be reproduced physically (holophony) but eventually the well-reproduced region becomes smaller than the size of a human head and decoding is generally switched to a max rE decoder, which is designed to optimise psychoacoustic cues.
The (slightly trippy) animation shows orders 1, 3, 5 and 7 of a 500 Hz sine wave to demonstrate the increasing size of the well-reconstructed region at the centre of the array. All of the loudspeakers interact to recreate the exact sound field at the centre but there is some unwanted interference out of the sweet spot.
Why HOA?
Since the number of loudspeakers has to at least match the number of HOA channels the cost and practicality are often the main limiting factor. How many people can afford 64 loudspeakers needed for a 7th order rendering? So why bother encoding things to a high order if we are limited to lower order playback? Two reasons: future-proofing and binaural.
First, future-proofing. One of the nice properties of HOA is that you can select a subset of channels to use for a lower order rendering. The first four channels in a fifth-order mix are exactly the same as the four channels of a first-order mix (see the spherical harmonic images above). We can easily ignore the higher order channels without having to do any approximative down-mixing. By encoding at a higher order than might be feasible at the minute you can remain ready for a future when loudspeakers cost the same as a cup of coffee (we can dream, right?)!
Second, binaural. If the limiting factors to HOA are cost and loudspeaker placement issues then what if we use headphones instead? A binaural rendering uses headphones to place a set of virtual loudspeakers around the listener. Now our rendering is only limited by the number of channels our PC/laptop/smartphone can handle at any one time (and the quality of the HRTF). The aXMonitor is an example of an Ambisonics-to-binaural decoder that can be loaded into any DAW that accepts VST format plugins, plug Pro Tools | Ultimate in AAX format.
The Future
As first-order Ambisonics makes its way into the workflow of not just VR/AR but also music production environments, we’re already seeing companies preparing to introduce HOA. Facebook already includes a version of second-order Ambisonics in its Facebook 360 Spatial Workstation [edit: They are now up to third order!]. Google have stated that they are working to expand beyond first-order for YouTube. I have worked with VideoLabs to include third-order Ambisonics in VLC Media player. This is in the newest version of VLC.
Microphones for recording higher than first-order aren’t at the stage of being accessible to everyone yet, but there are tools, like the a7 Ambisonics Suite that will let you encoded mono signals up to seventh-order, as well as to process the Ambisonics signal. There are also up-mixers like Harpex if you want to get higher orders from existing first-order recordings.
All of this means that if you can encoded your work in higher orders now, you should. You do not want to have to go back to your projects to rework them in six months or a year when you can do it now.

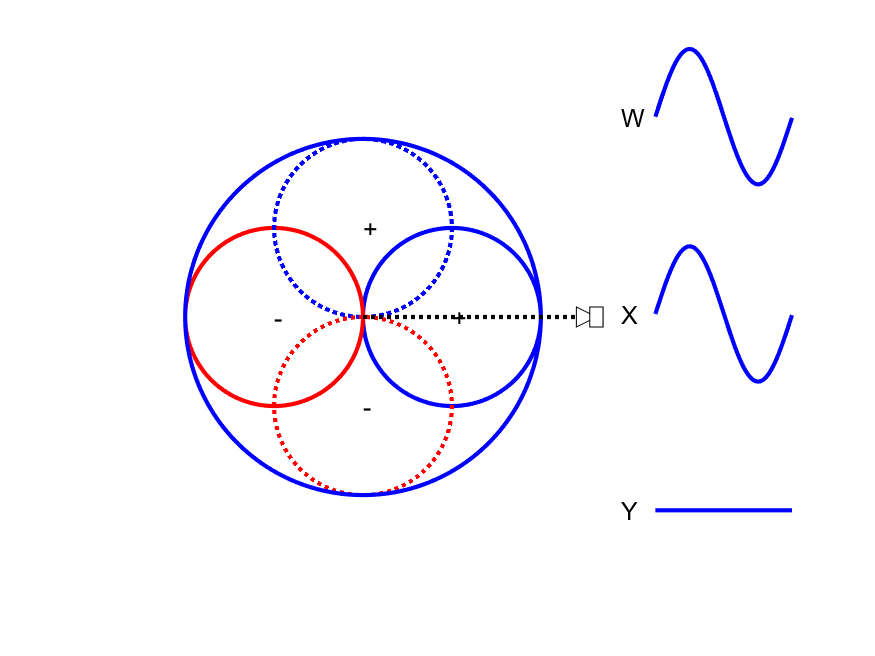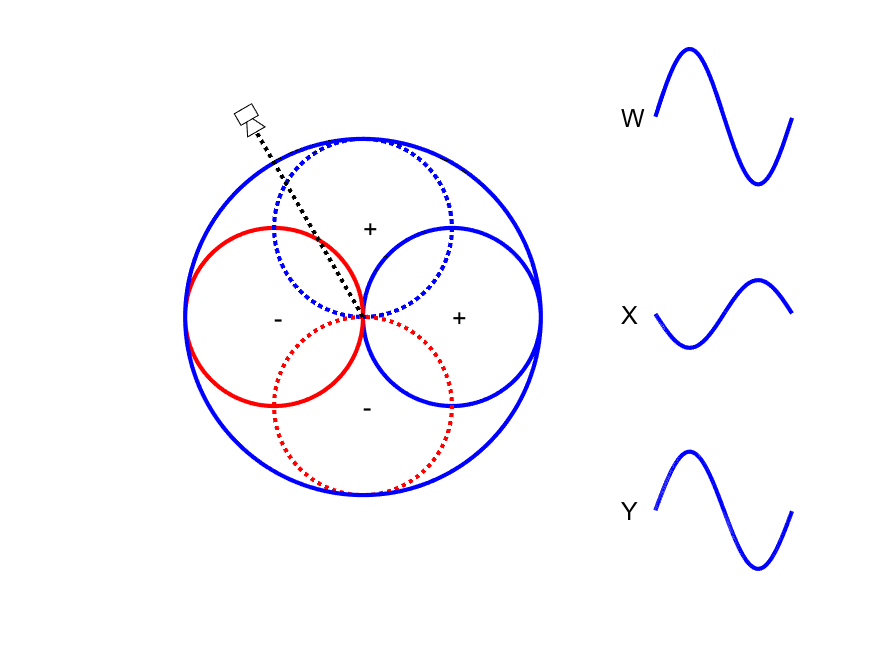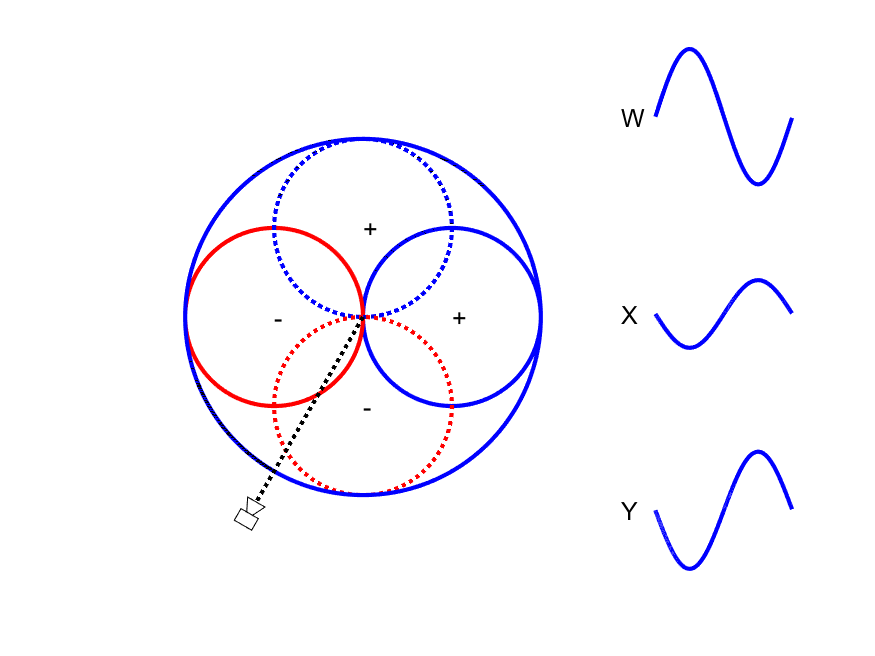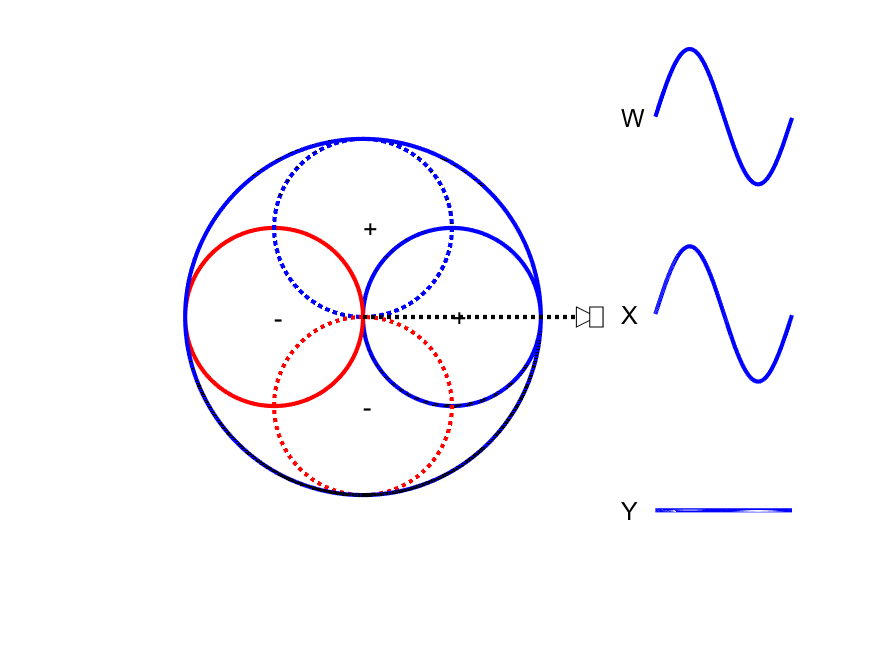 First-order Ambisonic encoding to SN3D for a sound source rotating in the horizontal plane. The Z channel is always zero for these source directions.
First-order Ambisonic encoding to SN3D for a sound source rotating in the horizontal plane. The Z channel is always zero for these source directions.